cours 3 : Le dessin vectoriel libre

Points abordés dans le cours :

Les courbes de Bézier

Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par Pierre Bézier (ingénieur Arts et Métiers et Supélec à la régie Renault dans les années 1950) qui les utilisait pour concevoir des pièces d'automobiles. Elles ont de nombreuses applications dans la synthèse d'images et le rendu de polices de caractères. Elles ont donné naissance à de nombreux autres objets mathématiques.

(sources : wikipédia / vous trouverez la description des équations mathématiques permettant la construction des courbes de Bézier sur la page qui leur est dédiée.)

Pour aller plus loin sur la conception des courbes de Bézier:

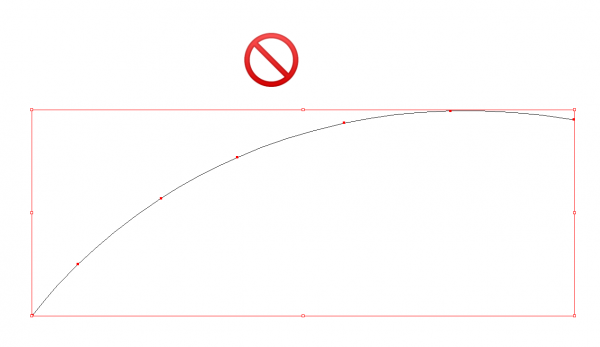
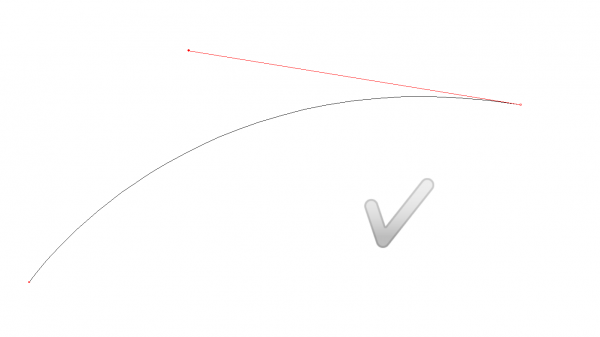
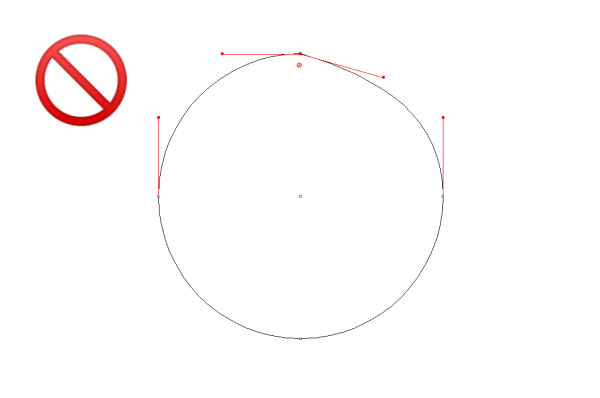
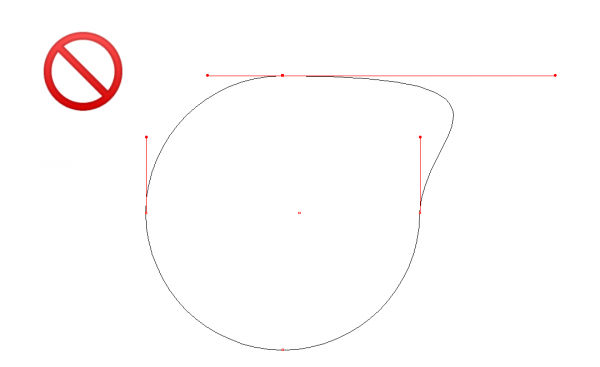
De manière générale, il faut toujours travailler dans une économie de points de vecteur. Une courbe de Bézier sera plus simple à construire avec 2 points d'ancrages qu'avec une multitude de points. Cela permettra de retravailler sa forme de manière plus rapide et plus précise. De plus, moins l'on a de points de vecteur, plus mon fichier vectoriel sera léger. Par exemple, dans le cas d'une découpe laser, si votre fichier comprend beaucoup de points d'ancrages inutiles, votre fichier pourra mettre bien plus de temps à être exécuté sur la machine.

Lorsque vous réalisez vos tracés il vous faut toujours prendre garde à équilibrer et aligner vos poignées de vecteurs afin que votre courbe de Bézier ne soit pas “cassée”.

le dessin vectoriel libre dans inkscape

outil tracer des courbes de Bézier et des segments de droites

raccourci ⟶ B

C'est l'outil principal de dessin libre de tracé vectoriel dans Inkscape. Il vous de tracer des chemin vectoriels en positionnant des points de vecteurs (en cliquant) eux même reliés par des tracés vectoriels (droits ou en courbe de Bézier selon votre dessin). C'est l'équivalent de l'outil Plume dans Illustrator.

Lorsque l'outil est sélectionné des options apparaissent dans le panneau supérieur:

⟶ Elles vous permettent de choisir un mode de dessin pour vos tracés vectoriels. Nous nous concentrerons sur le mode Créer un chemin de Bézier régulier mais n'hésitez pas à explorer les autres modes.

outil Éditer les nœuds ou les poignées de contrôle d'un chemin

raccourci ⟶ N

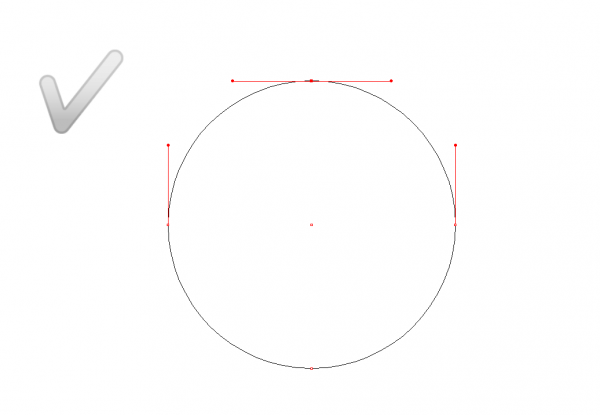
Comme son nom l'indique cet outil est essentiel pour un dessin vectoriel. Il vous permet de revenir sur un tracé en sélectionnant individuellement ou en groupe les points de vecteurs pour les déplacer ou agir sur des segments de votre tracé (par exemple pour y ajouter des points de vecteurs ou en supprimer). Il vous permet également de manipuler les poignées afin de travailler les courbes de Bézier de votre dessin. C'est un outil qui s'approche de l'outil de sélection direct dans Illustrator.

Lorsque l'outil est sélectionné des options apparaissent dans le panneau supérieur:

⟶ Celles-ci concernent les points de vecteurs. Elles vous permettent d'en ajouter ou d'en supprimer sur le tracé vectoriel sélectionné. Vous pouvez également relier ou briser un tracer vectoriel (l'équivalent du ciseau dans Illustrator).

⟶ Celles-ci vous permettent d'agir sur vos poignées. Par exemple le premier bouton de gauche sert à briser le tracer, c'est à dire rendre autonomes vos poignées d'un côté et de l'autre du point de vecteur. À l'inverse le second bouton liera équilibrera vos poignées.

⟶ Celle-ci transforment des éléments en chemins. Par exemple, de base Inkscape ne vous permet pas de manipuler le tracé vectoriel lorsque vous tracez une forme simple (comme un cercle, un rectangle ou un polygone). Pour se faire vous devez convertir ces objets en chemins. Vous pouvez le faire via le menu contextuel chemin⟶ objet en chemin ou bien utiliser le premier bouton de gauche qui est un raccourci. Le second bouton à droite qui vous permet de convertir vos contours en chemin comme nous l'avons vu en cours.

⟶ Enfin ces boutons concernent l'affichage de votre tracé. Je vous conseille de toujours avoir enclenché les boutons grisés sur cette image. Ils vous permettent de visualiser vos poignées et nœuds de contrôle.

Exercice à réaliser et à remettre pour le prochain cours

  1. À l'aide de l'outil plume et des différents outils étudiés jusqu'ici, redessinez la feuille d'une plante de votre choix (celles ci-dessous ne sont que des exemples) sur un format A3 (42×29,7cm)
  2. Votre dessin doit être correctement organisé sur différents calques identifiables (nommez-les!).
  3. Utilisez des tracés fermés et des tracés ouverts dans votre dessin.
  4. Votre dessin doit être en couleur
  5. Prenez un parti pris graphique franc (Allez le plus dans le détail possible dans votre illustration avec les ombres et nervures ou bien dans un style plus illustratif).
  6. 🚫 Pas de vectorisation dynamique 🚫

Quelques exemples de rendus précédents:

Et pour en voir encore d'autres, ici.